霍夫直线检测原理详解

在自动驾驶检测车道线的过程中，利用霍夫变换是实现车道线检测的一个思路，下面将来详细介绍霍夫直线检测的原理，首先明确霍夫变换的大体思想，其实就是利用坐标系的转换来产生一些神奇的效果。

我们先来看这样的一个例子，在直角坐标坐标系中有一点A(x0，y0)，则过该点的直线有无数条，我们称这些过该点的直线为一簇直线。那么这些直线的方程是什么呢？是的，该簇直线的方程为y0=kx0+b。

【我想这很容易理解，因为这些直线都过点(x0，y0)，但需要注意的是这里不同直线的k和b是不同时相等的 ，否则不就是一条直线了嘛】**我们上面得到了一簇直线的方程y0=kx0+b，现考虑将其换到另一个坐标系中对其进行表示，怎么理解呢，即我们将方程改写为b=-x0*k+y0。此时应变量是b，自变量是k，即上述方程是关于k-b的一个方程，而（x0，y0）是已知的点，则在k-b构成的坐标系下b=-x0*k+y0为一条直线。【注意：b-k坐标系我们称之为霍夫空间或参数空间，而原来直角坐标系空间称为图像空间】结合下图进行理解：

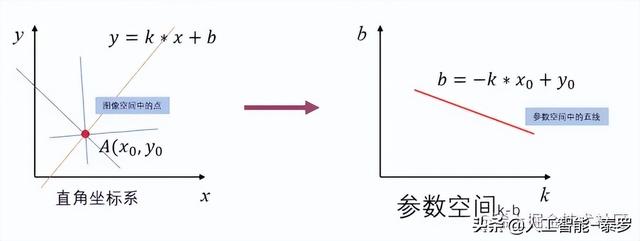
通过上例我想说明什么呢？**——图像空间x-y中的一点（x0，y0）对应于参数空间k-b中的一条直线b=-x0k+y0，也即图像空间中的点与参数空间中的直线一一对应。*

这里再来看一个例子，上文在图像空间有一点A(x0，y0)，此时确定了一簇直线。若再在图像空间中加入一点B(x1，y1)。

我们都知道两点确定一条直线，那么此时图像空间通过A、B两点就确定了一条直线，这样图像空间中的两点对应到参数空间表达了什么含义呢？可以简单地思考一下，图像空间中的一点对应参数空间中的一条直线，那么图像空间中的两点就对应参数空间中的俩条线呗，这两条线的交点会同时满足图像空间两点A、B所对应参数空间两条直线的方程。结合下图进行理解：

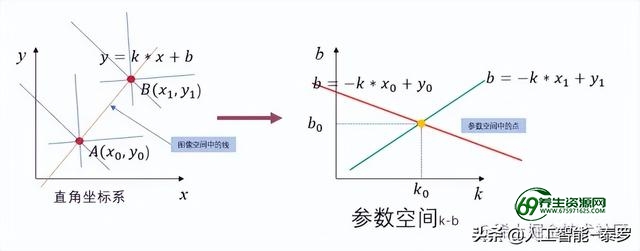
通过上例我又想说明什么呢？——图像空间中的一条直线AB对应于参数空间k-b中的一个点（k0，b0），也即图像空间中的直线与参数空间中的点一一对应。

通过上述例子我们得到了如下两条结论：

• 图像空间x-y中的一点对应于参数空间k-b中的一条直线。
• 图像空间中的一条直线对应于参数空间k-b中的一个点。

对于以上的两条结论我们能不能得出一些关于霍夫直线检测的思考呢？我想我们应该具备这样的能力，这里可以先不着急往下看哦，打开思路仔细想想，说不定会有不一样的发现呢。

既然我们知道了图像空间一条直线对应参数空间上的一个点，那么对于图像空间来说，只要一系列点在一条直线上，那么都会在参数空间上交与同一点；而不再同一条直线上的一系列点，它们对应于参数空间中的交点将会很凌乱，

即有许多不同的交点。【貌似这两句是废话一样，就是对之前结论的展开，我这么表述想表达什么呢？——即我们可以通过在参数空间中看哪些点是最多条直线的交点，那么这个交点对应直线所对应于图像空间中的一系列点将会是一条直线】**这里表述的稍微有点饶人，下面通过图来表达就一目了然了：

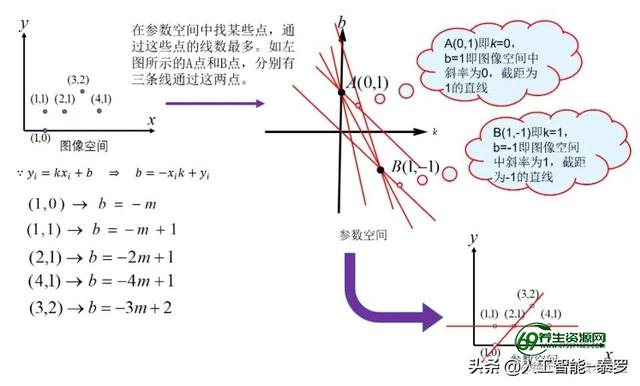
上图在图像空间中存在5个点，分别为（1，0）、（1，1）、（2，1）、（4，1）、（3，2）。然后这5个点将分别对应参数空间中的五条直线【直线方程在上图左下角】我们可以看出这五条直线有2个点是三条直线的交点，那么这两个交点分别对应于三条直线，而这三条直线对应于图像空间中的3点，可以发现这三点在一条直线上。这样我们就找出了图像空间中的直线。

通过上文的讲述，大家应该对霍夫直线检测有了一定的了解，即通过两个坐标空间之间的变换，将在图像空间中直线映射到参数空间的一个点，然后通过在参数空间里寻找峰值来完成直线检测任务。【这里的峰值意思是参数空间中最多的直线所交的那点】

大家通过上文的阅读，有没有发现什么漏洞呢？或者说有什么不严谨的地方呢？同样的，如果你发现了那说明你太棒了！没发现也可以先停下来思考思考，这会让你收获很大。

我们在讲第二个例子的时候【对应图2】有说这样的一句话：两条线的==交点==会同时满足图像空间两点A、B所对应参数空间两条直线的方程。可是在参数方程中的两条直线一定会存在交点嘛？如若不一定什么情况下会没有交点呢？我们知道的是若俩直线平行，也即斜率相等，则没有交点。现在参数空间中的直线方程为==b=-xi*k+yi==，其斜率为-xi 。由上分析可知，若在图像空间中两点的横坐标xi相等，则对应在参数空间中的直线平行，如下图所示：

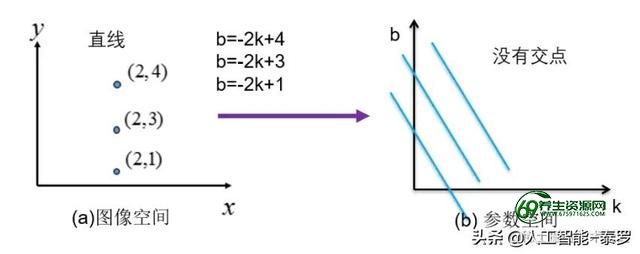
可以看出，当图像空间中3点的横坐标都为2时，对应的参数空间中的3条直线没有交点。

既然存在上述的缺陷，我们考虑换一种表示参数空间的方式——==采用极坐标表示==具体怎么将原先的直角坐标系（图像空间）转换到极坐标系（参数空间）呢？通过下图理解：

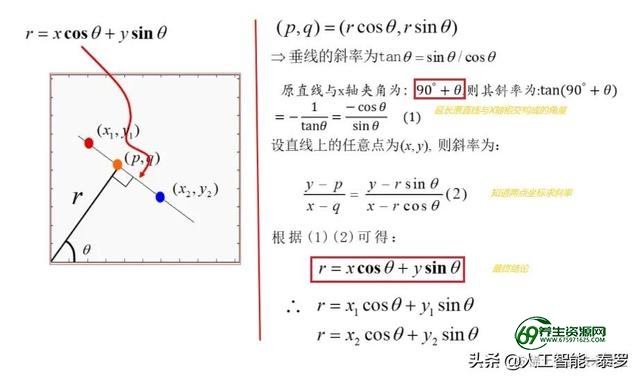
上图（p，q）点为坐标原点到(x1，y1)、(x2，y2)所在直线的垂点。我们联立两种计算斜率的方式公式，可以得到关于r和θ的极坐标方程：==r=xcosθ+ysinθ==。【注：这个方程式就类似于之前所说的==b=-xi*k+yi==，只是现在变成了极坐标系，其含义还是一致的】对于这个极坐标方程，同样的，参数空间的每个点（r，θ）都对应于图像空间的一条直线【（r，θ）已知，则r=xcosθ+ysinθ就是关于x,y的方程】；图像空间中的一个点（x，y）对应于参数空间中的一条曲线【（x，y）已知，则r=xcosθ+ysinθ就是关于r,θ的方程,其为一条曲线】。下图展示了从图像空间到极坐标参数空间的转换过程：

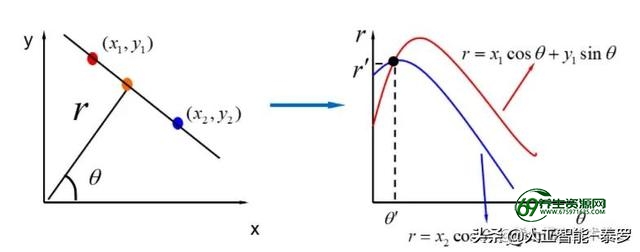
从上图可以看出：

• ==经过变换，图像空间中的每个点（x,y）被映射为极坐标空间的正弦曲线。==
• ==在图像空间中共线的点对应到极坐标空间会相交于一点（θ^'^,r^'^）。==

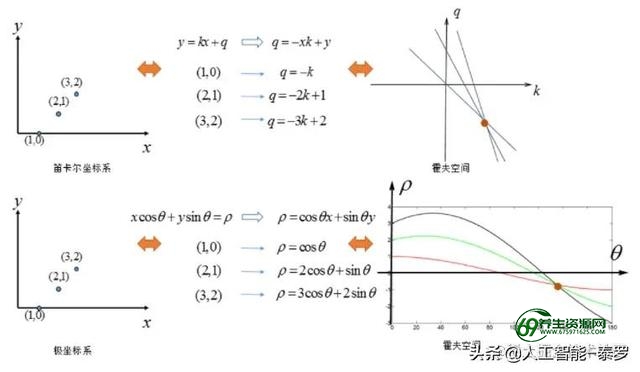
我们也可以来比较一哈直角坐标系空间转换到直角坐标系空间和直角坐标系空间转换到极坐标空间的区别，如下图所示：

霍夫直线检测的原理至此就全部讲完了，希望大家都能够理解【不能理解就多看几遍吧，我已经尽力在表达了】这里再次总结一下霍夫直线检测的原理——若一幅图像中的点构成一条直线，那么这些点在参数空间对应的曲线一定相交于一点，因此我们只需要将图像空间中的所有点变换到参数空间，得到一系列的曲线，然后我们只要检测这些曲线相交的点就可以确定直线了。

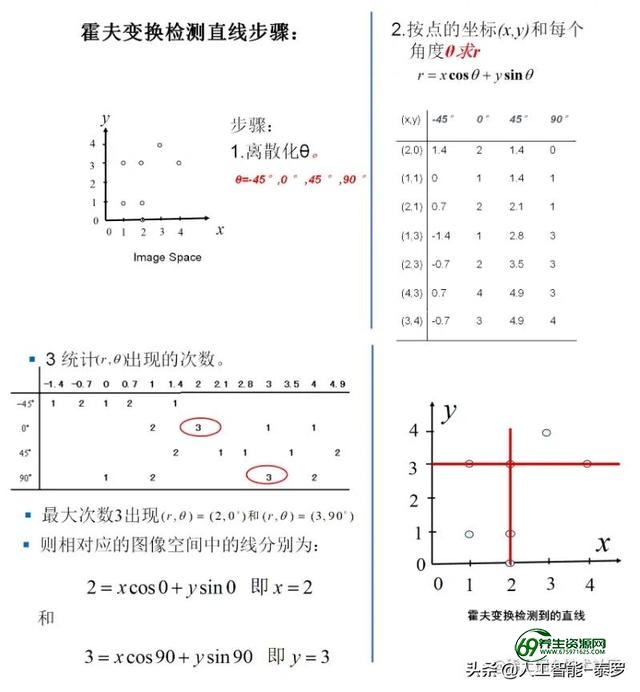
但是现在其实还是有些问题存在的，比如在一幅原始的图像中就没有完全在一条线上的点，即我们将这些点映射到参数空间后，多条直线共同的交点非常的少，几乎没有，那这样我们检测不到直线了。另一方面，我们计算很多条直线是否有共同的交点其实是不方便的，也比较消耗算力。因此，在实际过程中，我们往往将参数空间中的θ离散化为有限个等间距的离散值，这样参数r也就对应离散化为有限个值。然后我们会统计这些离散值r出现的频次来确实直线。听起来不好理解，通过下图理解：

呼呼呼~~到这里终于算是真正地把理论部分给介绍完了，在下一讲我将讲述霍夫直线检测的代码实战，敬请期待！

作者：秃头小苏
链接：https://juejin.cn/post/7089976897093763108
来源：稀土掘金